在Unity中创建基于Node节点的编辑器 (一)
本文共 34541 字,大约阅读时间需要 115 分钟。
孙广东 2018.5.13
Unity AssetStore中关于Node节点 编辑器相关的插件可是数不胜数, 状态机,行为树,Shader 可视化等等。
Unity自己也有 Animator的窗口使用, 还有新的Shader Graph。
现在Unity的编辑器代码已经开源了,还没有时间看。
第一部分, 创建界面 功能
在这篇博文中,我们将在Unity中创建我们自己的基于节点的编辑器。 是一个简单的节点编辑器,您可以进行改进。
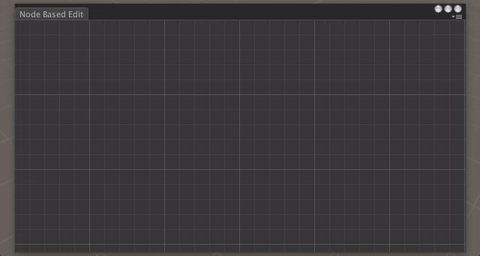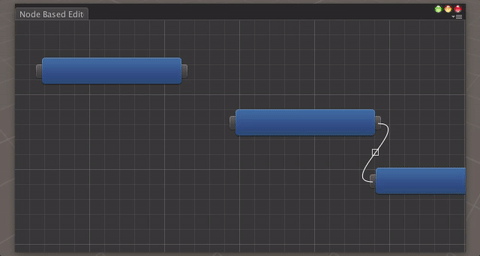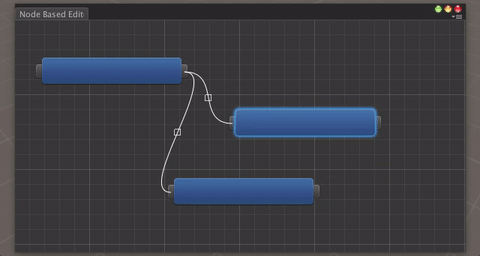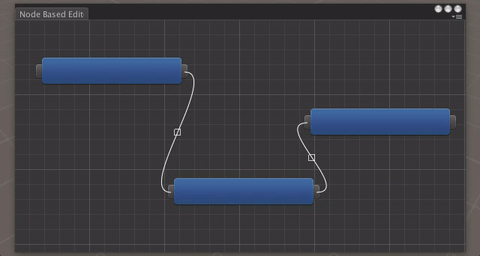
我们将在这篇文章中创建这个窗口(点击查看gif的动作)
创建窗口
我们先创建一个简单的编辑器窗口。 代码的结构与我们在之前的文章中开发的控制台克隆类似:首先绘制元素,然后处理输入,并且如果由于输入事件而改变GUI,则强制窗口重绘。
| using UnityEngine ; using UnityEditor ; using System . Collections . Generic ; public class NodeBasedEditor : EditorWindow { [ MenuItem ( "Window/Node Based Editor" )] private static void OpenWindow () { NodeBasedEditor window = GetWindow < NodeBasedEditor > (); window . titleContent = new GUIContent ( "Node Based Editor" ); } private void OnGUI () { DrawNodes (); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawNodes () { } private void ProcessEvents ( Event e ) { } } |
绘制节点
那么,因为这是一个节点编辑器,它应该包含一个节点列表,这就要求我们定义一个 List<Node>。 但首先我们应该定义Node类。 节点将负责绘制自己并处理自己的事件。 与 NodeBasedEditor中的 ProcessEvents(Event e) 不同,Node中的 ProcessEvents(Event e) 将返回一个布尔值,以便我们检查是否应该重新绘制GUI。
| using System ; using UnityEditor ; using UnityEngine ; public class Node { public Rect rect ; public string title ; public GUIStyle style ; public Node ( Vector2 position , float width , float height , GUIStyle nodeStyle ) { rect = new Rect ( position . x , position . y , width , height ); style = nodeStyle ; } public void Drag ( Vector2 delta ) { rect . position += delta ; } public void Draw () { GUI . Box ( rect , title , style ); } public bool ProcessEvents ( Event e ) { return false ; } } |
| using UnityEngine ; using UnityEditor ; using System . Collections . Generic ; public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; [ MenuItem ( "Window/Node Based Editor" )] private static void OpenWindow () { NodeBasedEditor window = GetWindow < NodeBasedEditor > (); window . titleContent = new GUIContent ( "Node Based Editor" ); } private void OnGUI () { DrawNodes (); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawNodes () { if ( nodes != null ) { for ( int i = 0 ; i < nodes . Count ; i ++ ) { nodes [ i ]. Draw (); } } } private void ProcessEvents ( Event e ) { } } |
创建节点
节点现在在编辑器中绘制,但如果我们不创建节点,则无法看到它们。 当用户在编辑器中点击右键时,我们应该显示一个带有“ Add node”项的上下文菜单。 当用户点击“ Add node”时,我们将创建一个节点并将其添加到节点列表中,以便绘制它。 节点需要位置,宽度,高度和样式; 位置将是鼠标的当前位置,宽度将是200,高度将是50(是的,我不喜欢在代码中使用 magic numbers,但这将是一个简单的编辑器),我们将复制Animator窗口的节点样式进行造型。
| using UnityEngine ; using UnityEditor ; using System . Collections . Generic ; public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; private GUIStyle nodeStyle ; [ MenuItem ( "Window/Node Based Editor" )] private static void OpenWindow () { NodeBasedEditor window = GetWindow < NodeBasedEditor > (); window . titleContent = new GUIContent ( "Node Based Editor" ); } private void OnEnable () { nodeStyle = new GUIStyle (); nodeStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/node1.png" ) as Texture2D ; nodeStyle . border = new RectOffset ( 12 , 12 , 12 , 12 ); } private void OnGUI () { DrawNodes (); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawNodes () { if ( nodes != null ) { for ( int i = 0 ; i < nodes . Count ; i ++ ) { nodes [ i ]. Draw (); } } } private void ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 1 ) { ProcessContextMenu ( e . mousePosition ); } break ; } } private void ProcessContextMenu ( Vector2 mousePosition ) { GenericMenu genericMenu = new GenericMenu (); genericMenu . AddItem ( new GUIContent ( "Add node" ), false , () => OnClickAddNode ( mousePosition )); genericMenu . ShowAsContext (); } private void OnClickAddNode ( Vector2 mousePosition ) { if ( nodes == null ) { nodes = new List < Node > (); } nodes . Add ( new Node ( mousePosition , 200 , 50 , nodeStyle )); } } |
使节点可拖动
好的,现在我们可以添加节点了,但是我们不能拖动它们。 正如我前面提到的,节点将处理它们自己的事件,因此我们将在 Node类中处理拖动事件。 这里需要注意的一点是,我们应该使用 Use() 方法“ using”拖动事件。 稍后,我们将添加画布拖动,并且我们不希望同时拖动节点和整个画布(“ using”一个事件阻止它被其他过程使用,即停止事件冒泡)。 另请注意, ProcessNodeEvents(Event e)中的for循环向后遍历节点列表,因为最后一个节点位于顶部,所以它应该首先处理事件。
| using System ; using UnityEditor ; using UnityEngine ; public class Node { public Rect rect ; public string title ; public bool isDragged ; public GUIStyle style ; public Node ( Vector2 position , float width , float height , GUIStyle nodeStyle ) { rect = new Rect ( position . x , position . y , width , height ); style = nodeStyle ; } public void Drag ( Vector2 delta ) { rect . position += delta ; } public void Draw () { GUI . Box ( rect , title , style ); } public bool ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { if ( rect . Contains ( e . mousePosition )) { isDragged = true ; GUI . changed = true ; } else { GUI . changed = true ; } } break ; case EventType . MouseUp : isDragged = false ; break ; case EventType . MouseDrag : if ( e . button == 0 && isDragged ) { Drag ( e . delta ); e . Use (); return true ; } break ; } return false ; } } |
NodeBaseEditor.cs
| private void OnGUI () { DrawNodes (); ProcessNodeEvents ( Event . current ); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawNodes () { if ( nodes != null ) { for ( int i = 0 ; i < nodes . Count ; i ++ ) { nodes [ i ]. Draw (); } } } private void ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 1 ) { ProcessContextMenu ( e . mousePosition ); } break ; } } private void ProcessNodeEvents ( Event e ) { if ( nodes != null ) { for ( int i = nodes . Count - 1 ; i >= 0 ; i -- ) { bool guiChanged = nodes [ i ]. ProcessEvents ( e ); if ( guiChanged ) { GUI . changed = true ; } } } } private void ProcessContextMenu ( Vector2 mousePosition ) { GenericMenu genericMenu = new GenericMenu (); genericMenu . AddItem ( new GUIContent ( "Add node" ), false , () => OnClickAddNode ( mousePosition )); genericMenu . ShowAsContext (); } |
创建节点之间的连接
我们的节点编辑器现在有节点,但我们也应该能够连接它们。为了做到这一点,我们需要一个节点上的两个连接点(in和out)以及它们之间的连接。一个连接点有一个矩形(以便我们可以绘制它),有一个类型(in或out),有一个样式并引用它的父节点。因此,我们的 ConnectionPoint 类将是一个非常简单的类。在特定位置绘制按钮并在点击该按钮时执行操作。
另一方面,连接有两个连接点和一个动作来删除它。 Connection类比 ConnectionPoint简单得多,但它引入了一个新概念: Handles。该类实际上用于在场景视图中绘制3D GUI控件,但它是唯一具有贝塞尔绘图方法的类: Handles.DrawBezier(Vector3, Vector3, Vector3, Vector3, Color, Texture2D, float). 。它需要7个参数,前4个参数是位置控制(起始位置,结束位置,起始切线和终止切线),而其余的则决定贝塞尔的外观。 ( 这个就太方便了, 不需要引入第三方插件或者自己写了)
ConnectionPoint.cs
| using System ; using UnityEngine ; public enum ConnectionPointType { In , Out } public class ConnectionPoint { public Rect rect ; public ConnectionPointType type ; public Node node ; public GUIStyle style ; public Action < ConnectionPoint > OnClickConnectionPoint ; public ConnectionPoint ( Node node , ConnectionPointType type , GUIStyle style , Action < ConnectionPoint > OnClickConnectionPoint ) { this . node = node ; this . type = type ; this . style = style ; this . OnClickConnectionPoint = OnClickConnectionPoint ; rect = new Rect ( 0 , 0 , 10f , 20f ); } public void Draw () { rect . y = node . rect . y + ( node . rect . height * 0.5f ) - rect . height * 0.5f ; switch ( type ) { case ConnectionPointType . In : rect . x = node . rect . x - rect . width + 8f ; break ; case ConnectionPointType . Out : rect . x = node . rect . x + node . rect . width - 8f ; break ; } if ( GUI . Button ( rect , "" , style )) { if ( OnClickConnectionPoint != null ) { OnClickConnectionPoint ( this ); } } } } |
Connection.cs
| using System ; using UnityEditor ; using UnityEngine ; public class Connection { public ConnectionPoint inPoint ; public ConnectionPoint outPoint ; public Action < Connection > OnClickRemoveConnection ; public Connection ( ConnectionPoint inPoint , ConnectionPoint outPoint , Action < Connection > OnClickRemoveConnection ) { this . inPoint = inPoint ; this . outPoint = outPoint ; this . OnClickRemoveConnection = OnClickRemoveConnection ; } public void Draw () { Handles . DrawBezier ( inPoint . rect . center , outPoint . rect . center , inPoint . rect . center + Vector2 . left * 50f , outPoint . rect . center - Vector2 . left * 50f , Color . white , null , 2f ); if ( Handles . Button (( inPoint . rect . center + outPoint . rect . center ) * 0.5f , Quaternion . identity , 4 , 8 , Handles . RectangleCap )) { if ( OnClickRemoveConnection != null ) { OnClickRemoveConnection ( this ); } } } } |
绘图连接
由于 Connection 和 ConnectionPoint类已准备就绪,我们所要做的就是在Node类中绘制连接点并在NodeBasedEditor中绘制连接。 Node类中的更改将最小化; 我们将定义两个连接点,修改构造函数,以便我们可以传递样式和动作,并使用 Draw() 方法绘制它们。
但是, NodeBasedEditor 需要进行重大修改。首先,我们需要为连接点定义样式。你可以为它们两个使用单一的样式,但我希望它们看起来不同,所以我将为每个样式使用不同的样式。我们将在 OnEnable() 中初始化这些样式,就像我们初始化节点样式一样。
其次,我们需要跟踪点击的连接点,这样当用户选择一个进出时,我们应该在它们之间建立一个连接。这一步包括大部分增加:
- OnClickInPoint(ConnectionPoint) 处理点击入点。
- OnClickOutPoint(ConnectionPoint) 处理点击出点。
- OnClickRemoveConnection(Connection) 处理单击连接上的删除按钮。
- CreateConnection() 在选择入点和出点时创建连接。
- ClearConnectionSelection() 清除选定的点。
最后,我们需要在 OnGUI() 中绘制连接,就像我们绘制节点一样。
| using System ; using UnityEditor ; using UnityEngine ; public class Node { public Rect rect ; public string title ; public bool isDragged ; public ConnectionPoint inPoint ; public ConnectionPoint outPoint ; public GUIStyle style ; public Node ( Vector2 position , float width , float height , GUIStyle nodeStyle , GUIStyle inPointStyle , GUIStyle outPointStyle , Action < ConnectionPoint > OnClickInPoint , Action < ConnectionPoint > OnClickOutPoint ) { rect = new Rect ( position . x , position . y , width , height ); style = nodeStyle ; inPoint = new ConnectionPoint ( this , ConnectionPointType . In , inPointStyle , OnClickInPoint ); outPoint = new ConnectionPoint ( this , ConnectionPointType . Out , outPointStyle , OnClickOutPoint ); } public void Drag ( Vector2 delta ) { rect . position += delta ; } public void Draw () { inPoint . Draw (); outPoint . Draw (); GUI . Box ( rect , title , style ); } public bool ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { if ( rect . Contains ( e . mousePosition )) { isDragged = true ; GUI . changed = true ; } else { GUI . changed = true ; } } break ; case EventType . MouseUp : isDragged = false ; break ; case EventType . MouseDrag : if ( e . button == 0 && isDragged ) { Drag ( e . delta ); e . Use (); return true ; } break ; } return false ; } } |
| using UnityEngine ; using UnityEditor ; using System . Collections . Generic ; public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; private List < Connection > connections ; private GUIStyle nodeStyle ; private GUIStyle inPointStyle ; private GUIStyle outPointStyle ; private ConnectionPoint selectedInPoint ; private ConnectionPoint selectedOutPoint ; [ MenuItem ( "Window/Node Based Editor" )] private static void OpenWindow () { NodeBasedEditor window = GetWindow < NodeBasedEditor > (); window . titleContent = new GUIContent ( "Node Based Editor" ); } private void OnEnable () { nodeStyle = new GUIStyle (); nodeStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/node1.png" ) as Texture2D ; nodeStyle . border = new RectOffset ( 12 , 12 , 12 , 12 ); inPointStyle = new GUIStyle (); inPointStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn left.png" ) as Texture2D ; inPointStyle . active . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn left on.png" ) as Texture2D ; inPointStyle . border = new RectOffset ( 4 , 4 , 12 , 12 ); outPointStyle = new GUIStyle (); outPointStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn right.png" ) as Texture2D ; outPointStyle . active . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn right on.png" ) as Texture2D ; outPointStyle . border = new RectOffset ( 4 , 4 , 12 , 12 ); } private void OnGUI () { DrawNodes (); DrawConnections (); ProcessNodeEvents ( Event . current ); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawNodes () { if ( nodes != null ) { for ( int i = 0 ; i < nodes . Count ; i ++ ) { nodes [ i ]. Draw (); } } } private void DrawConnections () { if ( connections != null ) { for ( int i = 0 ; i < connections . Count ; i ++ ) { connections [ i ]. Draw (); } } } private void ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { ClearConnectionSelection (); } if ( e . button == 1 ) { ProcessContextMenu ( e . mousePosition ); } break ; } } private void ProcessNodeEvents ( Event e ) { if ( nodes != null ) { for ( int i = nodes . Count - 1 ; i >= 0 ; i -- ) { bool guiChanged = nodes [ i ]. ProcessEvents ( e ); if ( guiChanged ) { GUI . changed = true ; } } } } private void ProcessContextMenu ( Vector2 mousePosition ) { GenericMenu genericMenu = new GenericMenu (); genericMenu . AddItem ( new GUIContent ( "Add node" ), false , () => OnClickAddNode ( mousePosition )); genericMenu . ShowAsContext (); } private void OnClickAddNode ( Vector2 mousePosition ) { if ( nodes == null ) { nodes = new List < Node > (); } nodes . Add ( new Node ( mousePosition , 200 , 50 , nodeStyle , inPointStyle , outPointStyle , OnClickInPoint , OnClickOutPoint )); } private void OnClickInPoint ( ConnectionPoint inPoint ) { selectedInPoint = inPoint ; if ( selectedOutPoint != null ) { if ( selectedOutPoint . node != selectedInPoint . node ) { CreateConnection (); ClearConnectionSelection (); } else { ClearConnectionSelection (); } } } private void OnClickOutPoint ( ConnectionPoint outPoint ) { selectedOutPoint = outPoint ; if ( selectedInPoint != null ) { if ( selectedOutPoint . node != selectedInPoint . node ) { CreateConnection (); ClearConnectionSelection (); } else { ClearConnectionSelection (); } } } private void OnClickRemoveConnection ( Connection connection ) { connections . Remove ( connection ); } private void CreateConnection () { if ( connections == null ) { connections = new List < Connection > (); } connections . Add ( new Connection ( selectedInPoint , selectedOutPoint , OnClickRemoveConnection )); } private void ClearConnectionSelection () { selectedInPoint = null ; selectedOutPoint = null ; } } |
选择节点
当用户点击一个节点时,我们应该提供反馈,以便他们知道他们选择了哪个节点(或者是否有节点被选中)。 这在用户想要删除节点时很有用。
| using System ; using UnityEditor ; using UnityEngine ; public class Node { public Rect rect ; public string title ; public bool isDragged ; public bool isSelected ; public ConnectionPoint inPoint ; public ConnectionPoint outPoint ; public GUIStyle style ; public GUIStyle defaultNodeStyle ; public GUIStyle selectedNodeStyle ; public Node ( Vector2 position , float width , float height , GUIStyle nodeStyle , GUIStyle selectedStyle , GUIStyle inPointStyle , GUIStyle outPointStyle , Action < ConnectionPoint > OnClickInPoint , Action < ConnectionPoint > OnClickOutPoint ) { rect = new Rect ( position . x , position . y , width , height ); style = nodeStyle ; inPoint = new ConnectionPoint ( this , ConnectionPointType . In , inPointStyle , OnClickInPoint ); outPoint = new ConnectionPoint ( this , ConnectionPointType . Out , outPointStyle , OnClickOutPoint ); defaultNodeStyle = nodeStyle ; selectedNodeStyle = selectedStyle ; } public void Drag ( Vector2 delta ) { rect . position += delta ; } public void Draw () { inPoint . Draw (); outPoint . Draw (); GUI . Box ( rect , title , style ); } public bool ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { if ( rect . Contains ( e . mousePosition )) { isDragged = true ; GUI . changed = true ; isSelected = true ; style = selectedNodeStyle ; } else { GUI . changed = true ; isSelected = false ; style = defaultNodeStyle ; } } break ; case EventType . MouseUp : isDragged = false ; break ; case EventType . MouseDrag : if ( e . button == 0 && isDragged ) { Drag ( e . delta ); e . Use (); return true ; } break ; } return false ; } } |
| using UnityEngine ; using UnityEditor ; using System . Collections . Generic ; public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; private List < Connection > connections ; private GUIStyle nodeStyle ; private GUIStyle selectedNodeStyle ; private GUIStyle inPointStyle ; private GUIStyle outPointStyle ; private ConnectionPoint selectedInPoint ; private ConnectionPoint selectedOutPoint ; [ MenuItem ( "Window/Node Based Editor" )] private static void OpenWindow () { NodeBasedEditor window = GetWindow < NodeBasedEditor > (); window . titleContent = new GUIContent ( "Node Based Editor" ); } private void OnEnable () { nodeStyle = new GUIStyle (); nodeStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/node1.png" ) as Texture2D ; nodeStyle . border = new RectOffset ( 12 , 12 , 12 , 12 ); selectedNodeStyle = new GUIStyle (); selectedNodeStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/node1 on.png" ) as Texture2D ; selectedNodeStyle . border = new RectOffset ( 12 , 12 , 12 , 12 ); inPointStyle = new GUIStyle (); inPointStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn left.png" ) as Texture2D ; inPointStyle . active . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn left on.png" ) as Texture2D ; inPointStyle . border = new RectOffset ( 4 , 4 , 12 , 12 ); outPointStyle = new GUIStyle (); outPointStyle . normal . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn right.png" ) as Texture2D ; outPointStyle . active . background = EditorGUIUtility . Load ( "builtin skins/darkskin/images/btn right on.png" ) as Texture2D ; outPointStyle . border = new RectOffset ( 4 , 4 , 12 , 12 ); } ... |
NodeBasedEditor.cs
| private void OnClickAddNode ( Vector2 mousePosition ) { if ( nodes == null ) { nodes = new List < Node > (); } nodes . Add ( new Node ( mousePosition , 200 , 50 , nodeStyle , selectedNodeStyle , inPointStyle , outPointStyle , OnClickInPoint , OnClickOutPoint )); } |
删除节点
一些节点编辑喜欢将节点按钮放在节点本身上,但在我们的情况下,这可能是危险的:用户可能会意外地删除节点。 所以,我们要做下一件最好的事情:将该按钮放在上下文菜单上。 用户应该首先选择节点,然后右键单击它以访问删除节点按钮。 当用户点击删除节点时,我们将从节点列表中删除该节点。 但是,该节点可能会连接到其他节点,所以我们应该首先删除这些连接。
| using System ; using UnityEditor ; using UnityEngine ; public class Node { public Rect rect ; public string title ; public bool isDragged ; public bool isSelected ; public ConnectionPoint inPoint ; public ConnectionPoint outPoint ; public GUIStyle style ; public GUIStyle defaultNodeStyle ; public GUIStyle selectedNodeStyle ; public Action < Node > OnRemoveNode ; public Node ( Vector2 position , float width , float height , GUIStyle nodeStyle , GUIStyle selectedStyle , GUIStyle inPointStyle , GUIStyle outPointStyle , Action < ConnectionPoint > OnClickInPoint , Action < ConnectionPoint > OnClickOutPoint , Action < Node > OnClickRemoveNode ) { rect = new Rect ( position . x , position . y , width , height ); style = nodeStyle ; inPoint = new ConnectionPoint ( this , ConnectionPointType . In , inPointStyle , OnClickInPoint ); outPoint = new ConnectionPoint ( this , ConnectionPointType . Out , outPointStyle , OnClickOutPoint ); defaultNodeStyle = nodeStyle ; selectedNodeStyle = selectedStyle ; OnRemoveNode = OnClickRemoveNode ; } public void Drag ( Vector2 delta ) { rect . position += delta ; } public void Draw () { inPoint . Draw (); outPoint . Draw (); GUI . Box ( rect , title , style ); } public bool ProcessEvents ( Event e ) { switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { if ( rect . Contains ( e . mousePosition )) { isDragged = true ; GUI . changed = true ; isSelected = true ; style = selectedNodeStyle ; } else { GUI . changed = true ; isSelected = false ; style = defaultNodeStyle ; } } if ( e . button == 1 && isSelected && rect . Contains ( e . mousePosition )) { ProcessContextMenu (); e . Use (); } break ; case EventType . MouseUp : isDragged = false ; break ; case EventType . MouseDrag : if ( e . button == 0 && isDragged ) { Drag ( e . delta ); e . Use (); return true ; } break ; } return false ; } private void ProcessContextMenu () { GenericMenu genericMenu = new GenericMenu (); genericMenu . AddItem ( new GUIContent ( "Remove node" ), false , OnClickRemoveNode ); genericMenu . ShowAsContext (); } private void OnClickRemoveNode () { if ( OnRemoveNode != null ) { OnRemoveNode ( this ); } } } |
NodeBasedEditor.cs
| private void OnClickAddNode ( Vector2 mousePosition ) { if ( nodes == null ) { nodes = new List < Node > (); } nodes . Add ( new Node ( mousePosition , 200 , 50 , nodeStyle , selectedNodeStyle , inPointStyle , outPointStyle , OnClickInPoint , OnClickOutPoint , OnClickRemoveNode )); } |
| private void OnClickRemoveNode ( Node node ) { if ( connections != null ) { List < Connection > connectionsToRemove = new List < Connection > (); for ( int i = 0 ; i < connections . Count ; i ++ ) { if ( connections [ i ]. inPoint == node . inPoint || connections [ i ]. outPoint == node . outPoint ) { connectionsToRemove . Add ( connections [ i ]); } } for ( int i = 0 ; i < connectionsToRemove . Count ; i ++ ) { connections . Remove ( connectionsToRemove [ i ]); } connectionsToRemove = null ; } nodes . Remove ( node ); } |
最后的接触
节点编辑器在这一点上是完整的,但它缺少一些可以提升用户体验的重要功能:
- 可拖动的画布,
- 从所选连接点到鼠标位置的贝塞尔曲线,
- 背景中的网格。
- 让我们的画布可以拖动是最简单的,所以让我们从这个开始。 我们所要做的只是将鼠标拖放到节点列表中的每个节点。
NodeBasedEditor.cs
| public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; private List < Connection > connections ; private GUIStyle nodeStyle ; private GUIStyle selectedNodeStyle ; private GUIStyle inPointStyle ; private GUIStyle outPointStyle ; private ConnectionPoint selectedInPoint ; private ConnectionPoint selectedOutPoint ; private Vector2 drag ; ... |
| private void ProcessEvents ( Event e ) { drag = Vector2 . zero ; switch ( e . type ) { case EventType . MouseDown : if ( e . button == 0 ) { ClearConnectionSelection (); } if ( e . button == 1 ) { ProcessContextMenu ( e . mousePosition ); } break ; case EventType . MouseDrag : if ( e . button == 0 ) { OnDrag ( e . delta ); } break ; } } |
| private void OnDrag ( Vector2 delta ) { drag = delta ; if ( nodes != null ) { for ( int i = 0 ; i < nodes . Count ; i ++ ) { nodes [ i ]. Drag ( delta ); } } GUI . changed = true ; } |
接下来,从所选连接点绘制贝塞尔到鼠标位置。 通过绘制这个贝塞尔曲线,我们将让用户知道选择了哪个连接点以及它们的连接将如何。
NodeBasedEditor.cs
| private void OnGUI () { DrawNodes (); DrawConnections (); DrawConnectionLine ( Event . current ); ProcessNodeEvents ( Event . current ); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } |
| private void DrawConnectionLine ( Event e ) { if ( selectedInPoint != null && selectedOutPoint == null ) { Handles . DrawBezier ( selectedInPoint . rect . center , e . mousePosition , selectedInPoint . rect . center + Vector2 . left * 50f , e . mousePosition - Vector2 . left * 50f , Color . white , null , 2f ); GUI . changed = true ; } if ( selectedOutPoint != null && selectedInPoint == null ) { Handles . DrawBezier ( selectedOutPoint . rect . center , e . mousePosition , selectedOutPoint . rect . center - Vector2 . left * 50f , e . mousePosition + Vector2 . left * 50f , Color . white , null , 2f ); GUI . changed = true ; } } |
最后,绘制网格:
| public class NodeBasedEditor : EditorWindow { private List < Node > nodes ; private List < Connection > connections ; private GUIStyle nodeStyle ; private GUIStyle selectedNodeStyle ; private GUIStyle inPointStyle ; private GUIStyle outPointStyle ; private ConnectionPoint selectedInPoint ; private ConnectionPoint selectedOutPoint ; private Vector2 offset ; private Vector2 drag ; ... |
| private void OnGUI () { DrawGrid ( 20 , 0.2f , Color . gray ); DrawGrid ( 100 , 0.4f , Color . gray ); DrawNodes (); DrawConnections (); DrawConnectionLine ( Event . current ); ProcessNodeEvents ( Event . current ); ProcessEvents ( Event . current ); if ( GUI . changed ) Repaint (); } private void DrawGrid ( float gridSpacing , float gridOpacity , Color gridColor ) { int widthDivs = Mathf . CeilToInt ( position . width / gridSpacing ); int heightDivs = Mathf . CeilToInt ( position . height / gridSpacing ); Handles . BeginGUI (); Handles . color = new Color ( gridColor . r , gridColor . g , gridColor . b , gridOpacity ); offset += drag * 0.5f ; Vector3 newOffset = new Vector3 ( offset . x % gridSpacing , offset . y % gridSpacing , 0 ); for ( int i = 0 ; i < widthDivs ; i ++ ) { Handles . DrawLine ( new Vector3 ( gridSpacing * i , - gridSpacing , 0 ) + newOffset , new Vector3 ( gridSpacing * i , position . height , 0f ) + newOffset ); } for ( int j = 0 ; j < heightDivs ; j ++ ) { Handles . DrawLine ( new Vector3 ( - gridSpacing , gridSpacing * j , 0 ) + newOffset , new Vector3 ( position . width , gridSpacing * j , 0f ) + newOffset ); } Handles . color = Color . white ; Handles . EndGUI (); } |
结论
结束。 您可以开发它并创建自己的自定义节点编辑器。 这是我在制作原型时编写的任务编辑器:

和往常一样,下面是完整的脚本。 直到下一次。
| using UnityEngine; using UnityEditor; using System.Collections.Generic; public class NodeBasedEditor : EditorWindow { private List<Node> nodes; private List<Connection> connections; private GUIStyle nodeStyle; private GUIStyle selectedNodeStyle; private GUIStyle inPointStyle; private GUIStyle outPointStyle; private ConnectionPoint selectedInPoint; private ConnectionPoint selectedOutPoint; private Vector2 offset; private Vector2 drag; [MenuItem("Window/Node Based Editor")] private static void OpenWindow() { NodeBasedEditor window = GetWindow<NodeBasedEditor>(); window.titleContent = new GUIContent("Node Based Editor"); } private void OnEnable() { nodeStyle = new GUIStyle(); nodeStyle.normal.background = EditorGUIUtility.Load("builtin skins/darkskin/images/node1.png") as Texture2D; nodeStyle.border = new RectOffset(12, 12, 12, 12); selectedNodeStyle = new GUIStyle(); selectedNodeStyle.normal.background = EditorGUIUtility.Load("builtin skins/darkskin/images/node1 on.png") as Texture2D; selectedNodeStyle.border = new RectOffset(12, 12, 12, 12); inPointStyle = new GUIStyle(); inPointStyle.normal.background = EditorGUIUtility.Load("builtin skins/darkskin/images/btn left.png") as Texture2D; inPointStyle.active.background = EditorGUIUtility.Load("builtin skins/darkskin/images/btn left on.png") as Texture2D; inPointStyle.border = new RectOffset(4, 4, 12, 12); outPointStyle = new GUIStyle(); outPointStyle.normal.background = EditorGUIUtility.Load("builtin skins/darkskin/images/btn right.png") as Texture2D; outPointStyle.active.background = EditorGUIUtility.Load("builtin skins/darkskin/images/btn right on.png") as Texture2D; outPointStyle.border = new RectOffset(4, 4, 12, 12); } private void OnGUI() { DrawGrid(20, 0.2f, Color.gray); DrawGrid(100, 0.4f, Color.gray); DrawNodes(); DrawConnections(); DrawConnectionLine(Event.current); ProcessNodeEvents(Event.current); ProcessEvents(Event.current); if (GUI.changed) Repaint(); } private void DrawGrid(float gridSpacing, float gridOpacity, Color gridColor) { int widthDivs = Mathf.CeilToInt(position.width / gridSpacing); int heightDivs = Mathf.CeilToInt(position.height / gridSpacing); Handles.BeginGUI(); Handles.color = new Color(gridColor.r, gridColor.g, gridColor.b, gridOpacity); offset += drag * 0.5f; Vector3 newOffset = new Vector3(offset.x % gridSpacing, offset.y % gridSpacing, 0); for (int i = 0; i < widthDivs; i++) { Handles.DrawLine(new Vector3(gridSpacing * i, -gridSpacing, 0) + newOffset, new Vector3(gridSpacing * i, position.height, 0f) + newOffset); } for (int j = 0; j < heightDivs; j++) { Handles.DrawLine(new Vector3(-gridSpacing, gridSpacing * j, 0) + newOffset, new Vector3(position.width, gridSpacing * j, 0f) + newOffset); } Handles.color = Color.white; Handles.EndGUI(); } private void DrawNodes() { if (nodes != null) { for (int i = 0; i < nodes.Count; i++) { nodes[i].Draw(); } } } private void DrawConnections() { if (connections != null) { for (int i = 0; i < connections.Count; i++) { connections[i].Draw(); } } } private void ProcessEvents(Event e) { drag = Vector2.zero; switch (e.type) { case EventType.MouseDown: if (e.button == 0) { ClearConnectionSelection(); } if (e.button == 1) { ProcessContextMenu(e.mousePosition); } break; case EventType.MouseDrag: if (e.button == 0) { OnDrag(e.delta); } break; } } private void ProcessNodeEvents(Event e) { if (nodes != null) { for (int i = nodes.Count - 1; i >= 0; i--) { bool guiChanged = nodes[i].ProcessEvents(e); if (guiChanged) { GUI.changed = true; } } } } private void DrawConnectionLine(Event e) { if (selectedInPoint != null && selectedOutPoint == null) { Handles.DrawBezier( selectedInPoint.rect.center, e.mousePosition, selectedInPoint.rect.center + Vector2.left * 50f, e.mousePosition - Vector2.left * 50f, Color.white, null, 2f ); GUI.changed = true; } if (selectedOutPoint != null && selectedInPoint == null) { Handles.DrawBezier( selectedOutPoint.rect.center, e.mousePosition, selectedOutPoint.rect.center - Vector2.left * 50f, e.mousePosition + Vector2.left * 50f, Color.white, null, 2f ); GUI.changed = true; } } private void ProcessContextMenu(Vector2 mousePosition) { GenericMenu genericMenu = new GenericMenu(); genericMenu.AddItem(new GUIContent("Add node"), false, () => OnClickAddNode(mousePosition)); genericMenu.ShowAsContext(); } private void OnDrag(Vector2 delta) { drag = delta; if (nodes != null) { for (int i = 0; i < nodes.Count; i++) { nodes[i].Drag(delta); } } GUI.changed = true; } private void OnClickAddNode(Vector2 mousePosition) { if (nodes == null) { nodes = new List<Node>(); } nodes.Add(new Node(mousePosition, 200, 50, nodeStyle, selectedNodeStyle, inPointStyle, outPointStyle, OnClickInPoint, OnClickOutPoint, OnClickRemoveNode)); } private void OnClickInPoint(ConnectionPoint inPoint) { selectedInPoint = inPoint; if (selectedOutPoint != null) { if (selectedOutPoint.node != selectedInPoint.node) { CreateConnection(); ClearConnectionSelection(); } else { ClearConnectionSelection(); } } } private void OnClickOutPoint(ConnectionPoint outPoint) { selectedOutPoint = outPoint; if (selectedInPoint != null) { if (selectedOutPoint.node != selectedInPoint.node) { CreateConnection(); ClearConnectionSelection(); } else { ClearConnectionSelection(); } } } private void OnClickRemoveNode(Node node) { if (connections != null) { List<Connection> connectionsToRemove = new List<Connection>(); for (int i = 0; i < connections.Count; i++) { if (connections[i].inPoint == node.inPoint || connections[i].outPoint == node.outPoint) { connectionsToRemove.Add(connections[i]); } } for (int i = 0; i < connectionsToRemove.Count; i++) { connections.Remove(connectionsToRemove[i]); } connectionsToRemove = null; } nodes.Remove(node); } private void OnClickRemoveConnection(Connection connection) { connections.Remove(connection); } private void CreateConnection() { if (connections == null) { connections = new List<Connection>(); } connections.Add(new Connection(selectedInPoint, selectedOutPoint, OnClickRemoveConnection)); } private void ClearConnectionSelection() { selectedInPoint = null; selectedOutPoint = null; } } |
| using System; using UnityEditor; using UnityEngine; public class Node { public Rect rect; public string title; public bool isDragged; public bool isSelected; public ConnectionPoint inPoint; public ConnectionPoint outPoint; public GUIStyle style; public GUIStyle defaultNodeStyle; public GUIStyle selectedNodeStyle; public Action<Node> OnRemoveNode; public Node(Vector2 position, float width, float height, GUIStyle nodeStyle, GUIStyle selectedStyle, GUIStyle inPointStyle, GUIStyle outPointStyle, Action<ConnectionPoint> OnClickInPoint, Action<ConnectionPoint> OnClickOutPoint, Action<Node> OnClickRemoveNode) { rect = new Rect(position.x, position.y, width, height); style = nodeStyle; inPoint = new ConnectionPoint(this, ConnectionPointType.In, inPointStyle, OnClickInPoint); outPoint = new ConnectionPoint(this, ConnectionPointType.Out, outPointStyle, OnClickOutPoint); defaultNodeStyle = nodeStyle; selectedNodeStyle = selectedStyle; OnRemoveNode = OnClickRemoveNode; } public void Drag(Vector2 delta) { rect.position += delta; } public void Draw() { inPoint.Draw(); outPoint.Draw(); GUI.Box(rect, title, style); } public bool ProcessEvents(Event e) { switch (e.type) { case EventType.MouseDown: if (e.button == 0) { if (rect.Contains(e.mousePosition)) { isDragged = true; GUI.changed = true; isSelected = true; style = selectedNodeStyle; } else { GUI.changed = true; isSelected = false; style = defaultNodeStyle; } } if (e.button == 1 && isSelected && rect.Contains(e.mousePosition)) { ProcessContextMenu(); e.Use(); } break; case EventType.MouseUp: isDragged = false; break; case EventType.MouseDrag: if (e.button == 0 && isDragged) { Drag(e.delta); e.Use(); return true; } break; } return false; } private void ProcessContextMenu() { GenericMenu genericMenu = new GenericMenu(); genericMenu.AddItem(new GUIContent("Remove node"), false, OnClickRemoveNode); genericMenu.ShowAsContext(); } private void OnClickRemoveNode() { if (OnRemoveNode != null) { OnRemoveNode(this); } } } |
| using System; using UnityEditor; using UnityEngine; public class Connection { public ConnectionPoint inPoint; public ConnectionPoint outPoint; public Action<Connection> OnClickRemoveConnection; public Connection(ConnectionPoint inPoint, ConnectionPoint outPoint, Action<Connection> OnClickRemoveConnection) { this.inPoint = inPoint; this.outPoint = outPoint; this.OnClickRemoveConnection = OnClickRemoveConnection; } public void Draw() { Handles.DrawBezier( inPoint.rect.center, outPoint.rect.center, inPoint.rect.center + Vector2.left * 50f, outPoint.rect.center - Vector2.left * 50f, Color.white, null, 2f ); if (Handles.Button((inPoint.rect.center + outPoint.rect.center) * 0.5f, Quaternion.identity, 4, 8, Handles.RectangleCap)) { if (OnClickRemoveConnection != null) { OnClickRemoveConnection(this); } } } } |
| using System; using UnityEngine; public enum ConnectionPointType { In, Out } public class ConnectionPoint { public Rect rect; public ConnectionPointType type; public Node node; public GUIStyle style; public Action<ConnectionPoint> OnClickConnectionPoint; public ConnectionPoint(Node node, ConnectionPointType type, GUIStyle style, Action<ConnectionPoint> OnClickConnectionPoint) { this.node = node; this.type = type; this.style = style; this.OnClickConnectionPoint = OnClickConnectionPoint; rect = new Rect(0, 0, 10f, 20f); } public void Draw() { rect.y = node.rect.y + (node.rect.height * 0.5f) - rect.height * 0.5f; switch (type) { case ConnectionPointType.In: rect.x = node.rect.x - rect.width + 8f; break; case ConnectionPointType.Out: rect.x = node.rect.x + node.rect.width - 8f; break; } if (GUI.Button(rect, "", style)) { if (OnClickConnectionPoint != null) { OnClickConnectionPoint(this); } } } } |
转载地址:http://qkla.baihongyu.com/
你可能感兴趣的文章
Objective-C实现排队叫号系统(附完整源码)
查看>>
Objective-C实现控制NRP8S功率计读取功率 (附完整源码)
查看>>